How the Overtone Series Works #
In its most basic sense sound is made up of waves. Those waves produce changes of pressure in the air, and our ears interpret those pressures as different pitches. Faster waves produce higher pitches, while slower waves produce lower pitches.
The overtone series is a natural phenomenon in which a single pitch produces multiple additional harmonic pitches through mathematical divisions. The set of resulting pitches form the basis for everything we do as jazz musicians.
Fundamentally, all western music, including jazz, is rooted in the overtone series. After all, unorganized sounds are just meaningless noise, whereas music is created through creative organization and compilation of sound.
As we will learn, the overtone series sets the stage for all the major components of modern music, from pitches, to chords, scales and even determines why a trumpet sounds different from a guitar.
This may sound like nerdy scientific mumbo-jumbo, and you may wonder why you should care about the inner workings of sound when you could just focus on which keys to press on your instrument. But, understanding these fundamental ideas really helped me explore my playing and expand my appreciation of music.
How Sound Waves Work #
Sound waves are measured by their frequency — the number of cycles each sound wave makes over time. Modern day standard tuning is based on a standard of A = 440hz, which is to say the note with a frequency of 440 cycles per second would create an “A” pitch.
Picture a string pulled tight between two points. When plucked, that string vibrates creating a wave pattern. The higher the strings tension, the faster the waves that it produces, which creates a higher pitch.
This is exactly how a string instrument like a guitar works. A guitar has six strings, each tuned to different pitches by tightening each string individually. A guitar player can change the pitch of the string while playing, by pressing the string against the fretboard. This shortens the string, changing it’s tension, which raises the pitch.
A Single Pitch Will Also Produce Overtone Pitches #

Step-by-Step Video Training
As a premium member of Jazz-Library you will have access to our Jazz Fundamentals video course which has 70+ video lessons teaching you comping rhythms, chord voicings, soloing strategies and more.
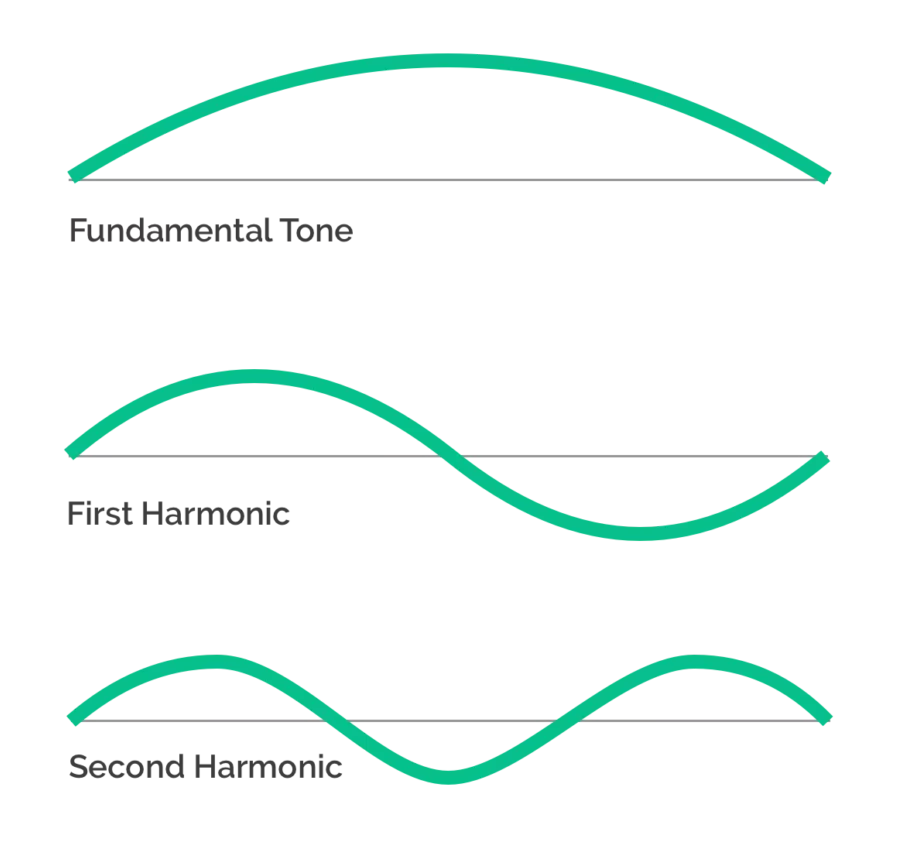
When played in nature, a single tone played by an instrument will produce several additional pitches which are related to it mathematically. For example, a string vibrating at 440hz will also produce a secondary vibration at double it’s frequency, 880hz, as well as others at higher multiples (3x, 4x and so on).
We call the originating frequency the “fundamental tone” and each of the secondary tones are called “overtones,” or “harmonics.”
Hear it for Yourself #
If you have access to an acoustic piano, there’s a really simple exercise you can do to hear these overtones for yourself. Since the piano is made up of many strings, tuned to different frequencies, pressing one key will cause other notes within it’s harmonic series to sound as well.
To hear it for yourself, sit at the piano, and press a key very gently so it doesn’t make a sound and hold it. By doing this you are lifting the pad that mutes that string, allowing it to vibrate freely. With that key still held, strike higher octaves of the same note with a strong attack. You will hear multiple pitches sounding all from the same string .
This demonstrates sympathetic resonance. The pressure waves which result from the strings you strike, cause the one you are holding to vibrate as well.
What Makes Instruments Sound Unique? #
When sounded, each fundamental pitch produces a predictable set of harmonics. This is true regardless of the instrument that is playing. That said, a guitar and piano sound distinctly different from each other. Why is that?
Those differences are explained through timbre and resonance. Each of those are deep topics on their own, but simply put, the construction of the instruments blend their overtimes differently, which produce a unique quality for that instrument. Timbre explains why a trumpet and flute sound distinctly different, where resonance describes why two different acoustic guitars sound similar, but with subtle tone differences.
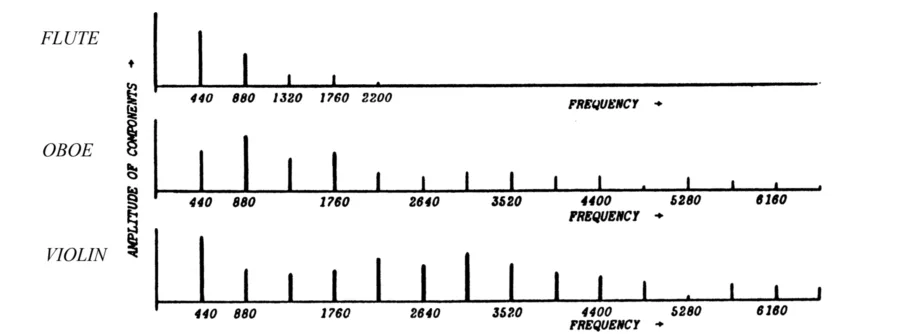
If we were to take a single C4 pitch and play it on different instruments, we would see the same overtones produced but at different volumes. In this example, you can see that a flute only has a few overtones that are audible, where a violin has far more. This is a key factor in why the two instruments sound different when playing the same pitch.
Overtone Series #
The overtones produced from a single fundamental pitch are predictable. They are the result of a relatively straight forward mathematical function. This function calculates the overtones as the tone a double the frequency of the fundamental pitch, + 1/2 the frequency, + 1/3, +1/4, and so on.
| Pitch | Function | Frequency |
|---|---|---|
| A | Fundamental | 110hz |
| A | 1st overtone | 220hz |
| E | 2nd overtone | 330hz |
| A | 3rd overtone | 440hz |
| C# | 4th overtone | 550hz |
| E | 5th overtone | 660hz |
Here’s a more complete look at the same harmonic series notated on a staff:

Tuning Systems #
While tuning systems are a whole topic of themselves, we can’t explore much more without a passing explanation of just intonation vs. equal temperament.
The overtones produced via the harmonic series will be tuned perfectly to the fundamental. This perfect mathematical alignment is known as just intonation, and results in the most “in tune” notes.
But, just intonation has some practical application problems. That is, different fundamental pitches will contain some of the same notes in their overtone series, but the resulting wave frequencies will not be identical.
As an example, the note E in our example of the A harmonic series is 330hz, but the same E in the harmonic series for C is 327hz. As you play a musical line, or in an ensemble, your note E will need to be tuned differently depending on it’s function.
For instruments which can vary their tuning on the fly, playing in this way is just fine. For this reason, it’s quite common for vocal choirs or string quartets to play in just intonation.
But, when it comes to instruments which cannot vary their tuning as they play, just intonation is impossible to achieve. Pianos, guitars, organs, harps, and other similar instruments must compromise their tuning to be practical to play.
The result of that compromise is the equal temperament tuning system, in which notes are “rounded” to a common frequency so that a single frequency is assigned to each note, so that it sounds reasonably in tune across all it’s functions.
The following staff shows the same overtone series as before, but notating the difference in pitch between just intonation and equal temperament.

Musical Intervals Derived from the Harmonic Series #
The notes of the harmonic series are stacks of intervals, with each interval getting asymptotically smaller as the series goes on.
The first two notes form an octave, followed by a perfect fifth, a perfect fourth, a major third, a minor third, a major second, and so on. All together, these spell out the intervals behind our music.
The intervals early in the series sound consonant, with intervals becoming increasingly dissonant as you progress through the series. As musicians, we use these consonant and dissonant qualities to create engaging music. Chords constructed of consonant intervals sound pleasing and natural (eg. major and minor), while chords of dissonant intervals are unstable and unnerving (eg, dominant and diminished).
As jazz musicians, we exploit this by taking our listeners on a journey between consonant sounds, into unstable dissonant sounds, and resolve back to consonance.
In fact, I would argue that one of the fundamental differences between classical and jazz musicians, is their tolerance for dissonance.
Related Ideas to Explore #
Throughout the articles on this website you will find many places where we apply the foundation of the harmonic series to new ideas. The more you study, the more you’ll realize that the possibilities are endless.