Using Tonnetz Tone Mesh To Understand Jazz Harmony

Researchers say that roughly 65% of people are visual learners. For those people, visualizing concepts help build a more solid understanding of how something works. Much in the same way a chart helps us understand a complex spreadsheet of data, a Tonnetz gives us a simple visual of the complex mathematics behind music.

So, what is a Tonnetz? The Tonnetz is a 2-dimensional mesh which maps the tonal landscape of western music. It was created back in 1739 by Leonhard Euler as a way to graphically represent the ideas behind Neo-Riemannian theory.

It’s most often used as a technique for analyzing European music, particularly from the unique chord progressions of the Romantic period. Similarly, I find it helps me better understand the often complex structure of Jazz standards.

What you Can Learn from a Tonnetz #

By learning how a Tonnetz works, you’ll be able to visually accomplish the following fundamental music theory tasks.

• You’ll be able to quickly find the notes to any chord.
• You’ll be able to identify what notes are in each key.
• You’ll be able to transpose chord progressions into other keys.
• You’ll be able to find relative major and minor chords
• You’ll be able to identify substitute chords with common chord tones
• You can find many chord options that fit a common note, perhaps the melody note.

How the Tonnetz is Constructed #

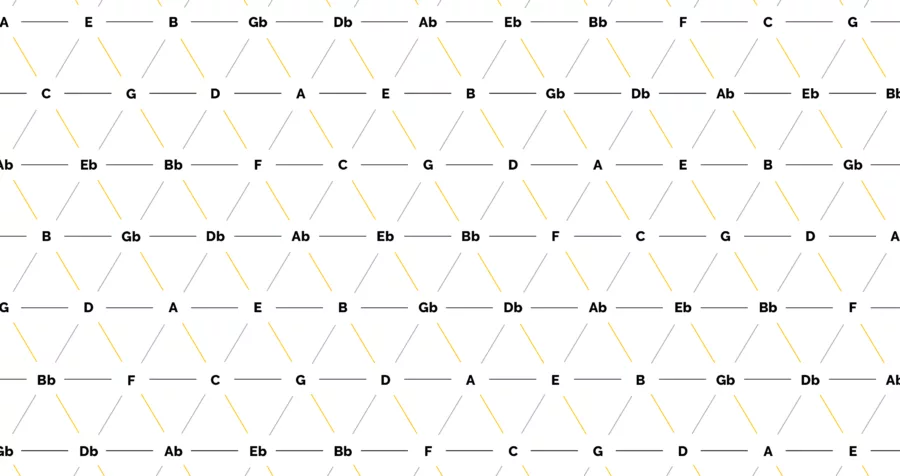
Let’s have a look at the Tonnetz. It’s a mesh of triangles with notes at the intersecting points. The edges of the triangles form lines, which represent intervals between the notes. The mesh knows no bounds, continuing on infinitely in all directions.

Download my printable tonnetz worksheet to follow along.

Horizontal Lines #

Look first at the horizontal grid lines. The notes along each of these lines progress in Perfect 5ths from left to right. As such, each of these lines is like a flattened Circle of Fifths, extending endlessly in both directions.

Diagonal Lines #

The diagonal grid lines in grey, which move up and to the right, create major-3rd intervals. (Highlighted in Blue below).

The opposing diagonal grid lines, in orange, are minor-3rd intervals. (Highlighted in Green).

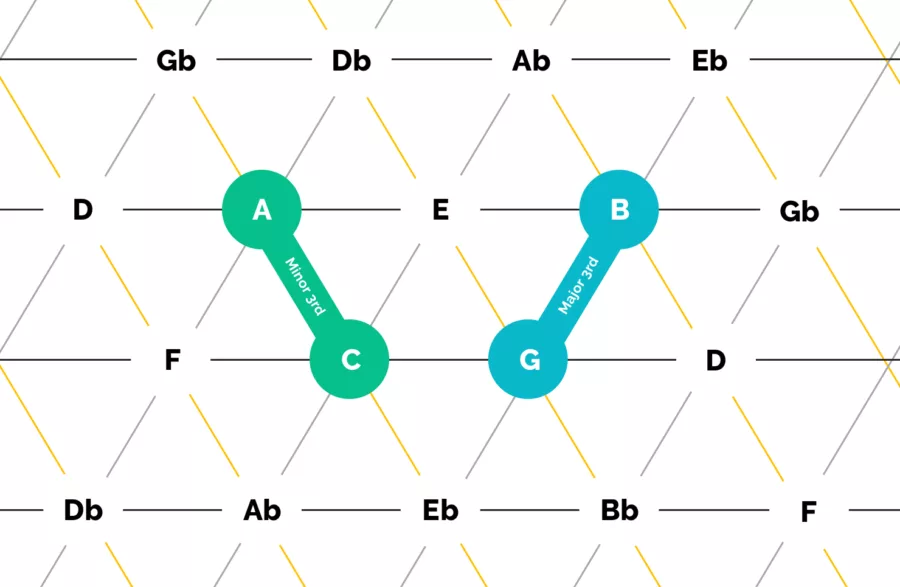
These construction rules reveal the first lesson that we can learn from the Tonnetz. That is, a Perfect 5th is the result of adding together a Major 3rd and Minor 3rd.

Building Chords Using Shapes #

Our basic major and minor triads are both constructed using a Perfect 5th, a Major 3rd and a Minor 3rd, and as such, they fit perfectly nicely on the mesh as triangles.

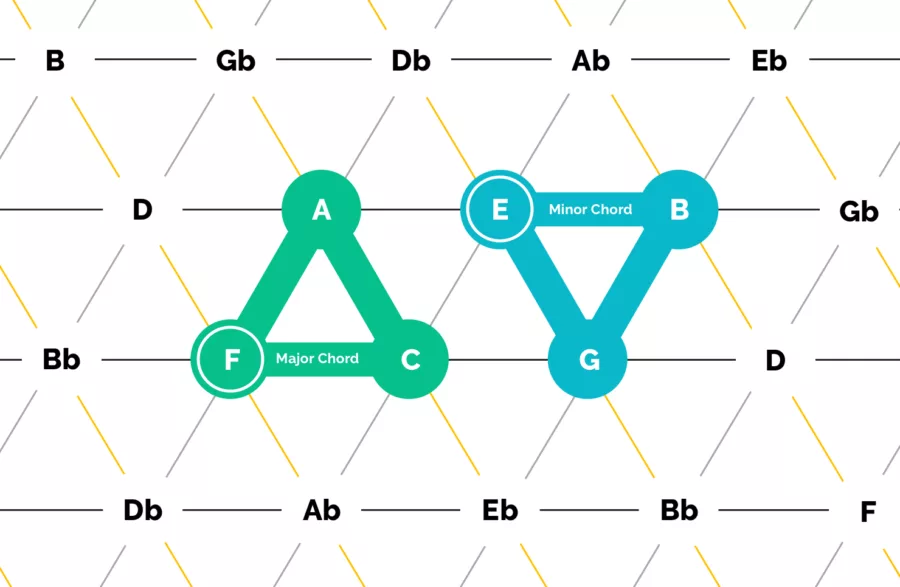
The major triad, with the major 3rd on the bottom, can be drawn as a triangle with the point on top, as in green above.

Along the same lines, a minor triad is a triangle with the point on the bottom, as in blue.

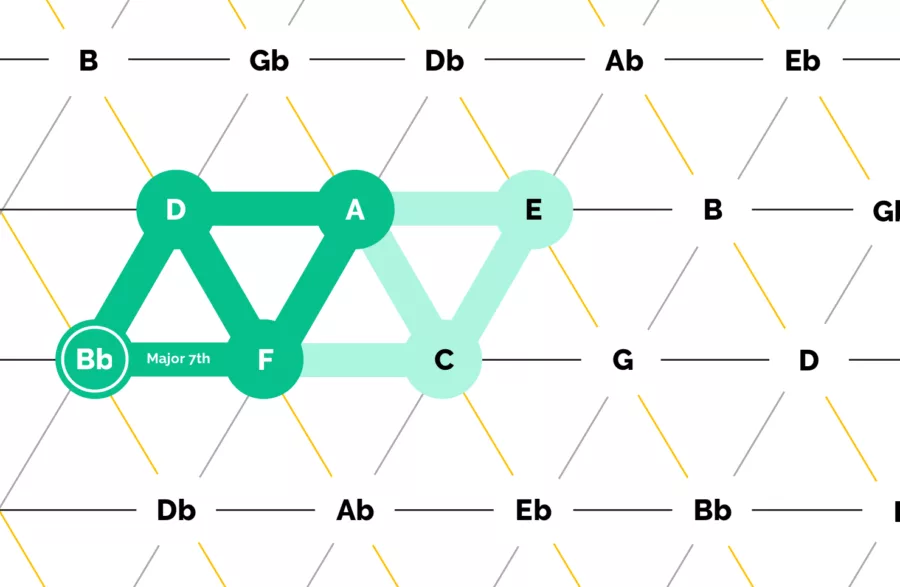
Major and Minor 7th Chords #

Continuing with this logic, our major and minor 7th chords each add a 4th note to the chord. In a major chord, the added note is a major 3rd above the chord, and for a minor 7th, we add a the note a minor 3rd above instead.

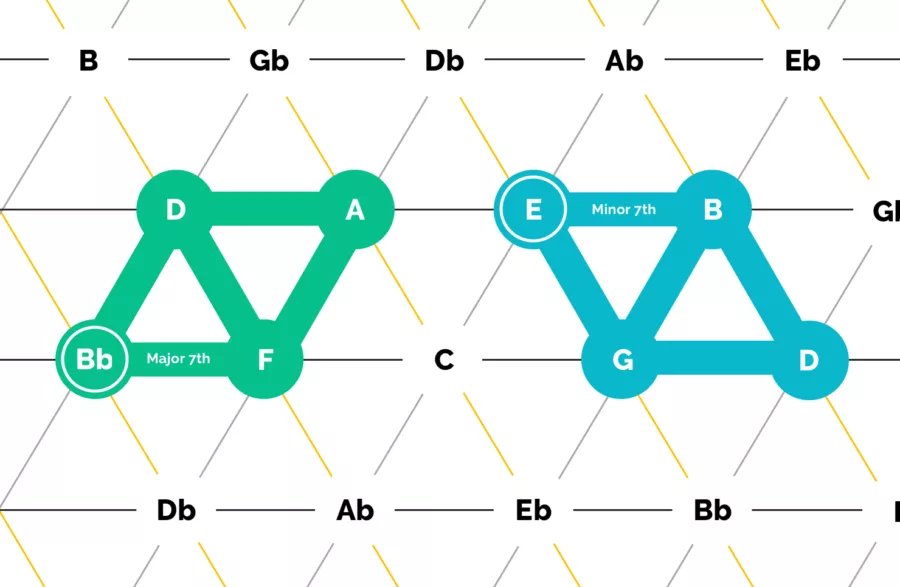
When you visualize these major chords and minor 7th chords, you see an interesting pattern — they are just a merging of a major chord with a minor chord together into a single chord.

Dominant, Diminished and Half-Diminished #

Up to this point all of the shapes have formed closed shapes on the mesh. As you experiment more, you’ll find that consonant chords are closed shapes, and dissonant chords have dangly bits hanging off them.

To show how this works, let’s look at the most dissonant chord there is, the diminished chord, in blue.

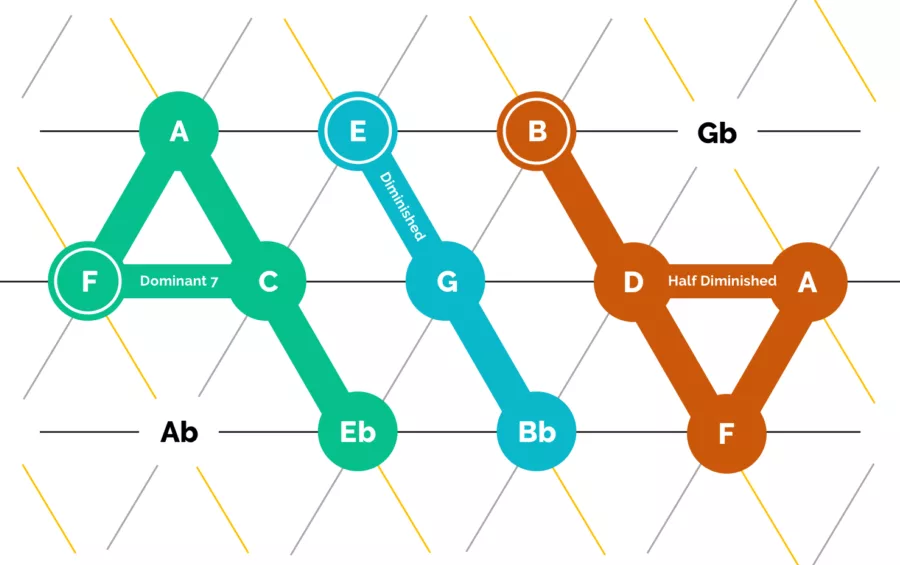
The diminished chord moves in a straight line down and to the right, stacking minor 3rds. While not pictured here, it has a sibling chord which moves in a straight line up and to the right, stacking major 3rds, which we call augmented. Both chords function the same way. They don’t make a closed shape, so it really wants to morph into a consonant shape to resolve.

A dominant 7th chord (green) is a merging of the major triad with a diminished chord. Similarly, a half-diminished chord (aka, “m7b5”), shown in brown, is the combination of a diminished chord and a minor chord.

Both of these chords have consonant shapes, but have unresolved dangly bits hanging off of them. They have tension and need to move or change to sound fully resolved.

To resolve those chords you “sever the tail” by pulling them away from the dangling note. For example, the green dominant 7th chord (F7) wants to resolve by shedding that tail (Eb) and shifting the triangle to the left 1 slot, landing on a Bb major triad. The half-diminished does the same thing, in the opposite direction, moving the triangle from a B half-diminished, to Amin.

This is why I love the Tonnetz. These shapes and movement illustrate that a half-diminished chord and dominant-7th chord are mathematically the same concept, just resolving their leading tones in opposite directions.

Keys, Scales and Modes #

We can also use the Tonnetz to define the key we are playing in. To do that, have a look at a major scale:

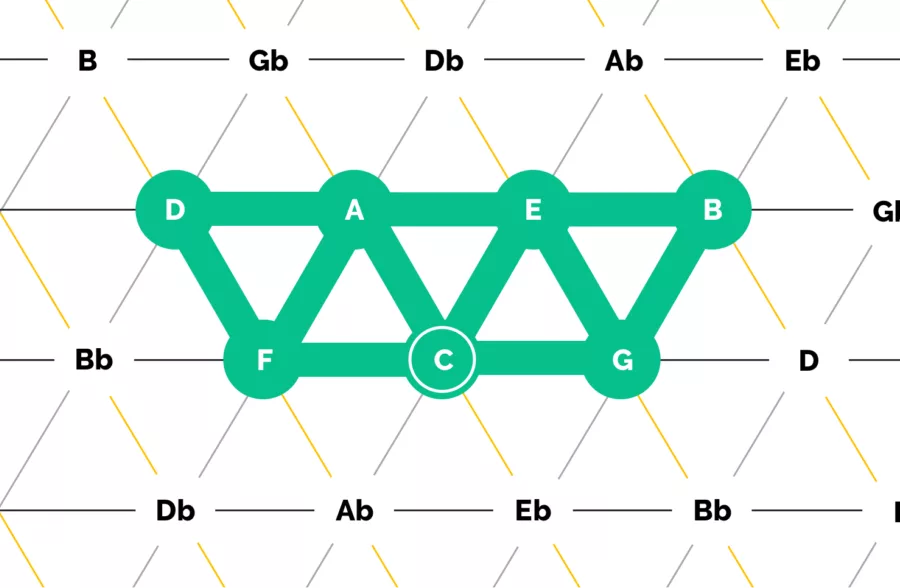
The first thing you may notice is that it makes a nice closed shape, without any dangly bits. The notes of the major scale are consonant with each other, part of a family.

The next you you should notice is that the major scale is made entirely of triangles, which form major and minor triads. Specifically, 3 minor triads and 3 major. (The 3rd on is a little hard to see, as the D in the G maj chord is not highlighted since it’s already included on the top left, but it makes the same nice triangle shape.)

Next the minor scale:

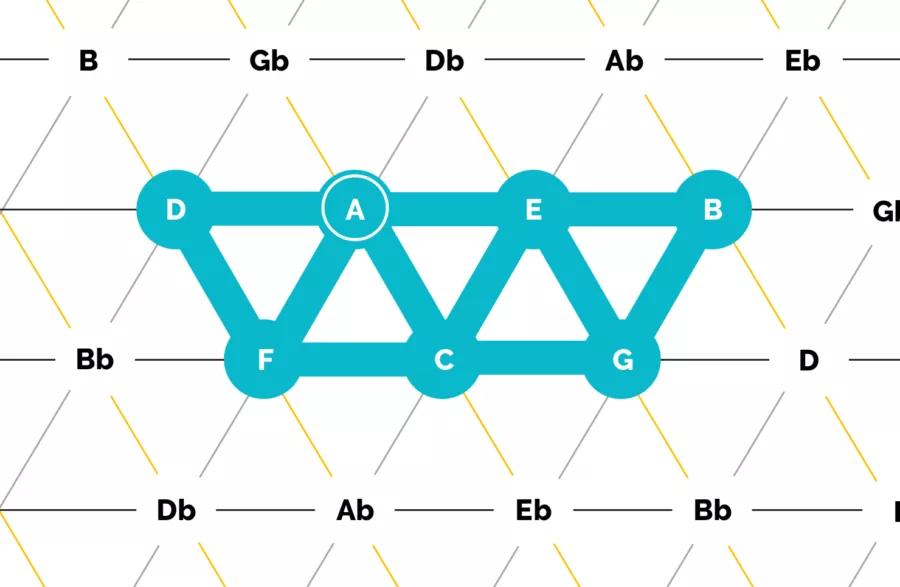
Wait a minute… isn’t that the same shape and notes as the major scale? Indeed! The minor scale contains the same notes as it’s relative major. The only difference is which note you start on. In this case, I’ve added a white circle to indicate the A is the key center here, vs. the C in the previous major diagram.

And thus, another lesson is learned from the Tonnetz. In fact, all of the major modes are contained in this shape, as they all contain the same notes. The only difference is in which note you decide to designate as the key center.

Moving Around the Circle of Fifths #

You may have heard jazz musicians talk about brightening or darkening their music by adding or removing notes around the circle of fifths. Traditionally it is taught that adding “sharps” by moving clockwise around the circle will “brighten” the music, while adding “flats” by moving counter-clockwise will “darken” it.

This works on the Tonnetz too. Since our horizontal lines are just a flattened out Circle of Fifths, we can brighten our chords by adding notes that extend off the right side. Likewise, we can darken by adding notes on the left.

Just remember, if you want to keep your chord consonant, make sure you add notes by building new triangles. If you add a dangly bit, your chord will be dissonant.

Transposing #

By now you should realize that the chord shapes are all the same, irregardless of the key you are in. Similarly, the tonal mesh is perfectly consistent in its construction.

Because of this, you can plot out the chords of your song on the Tonnetz, and then shift them all uniformly onto other notes. As long as the relative shapes and distance don’t change as you move them, your song will stay in tact, albeit, now in a new key.

Negative Harmony #

As a final demonstration of the awesomeness of the Tonnetz, let’s play with negative harmony. Negative harmony is too deep of a topic to explain in the context of this article. But, if you have an understanding of the concept already, it’s a fun topic to explore visually on the mesh. If this is over your head, don’t worry, it’s a super nerdy topic which isn’t often taught in traditional music channels.

First, identify your key center. In this case, I’ve picked the key of C major, and I’ve drawn in green a G7 chord, the dominant chord in the key.

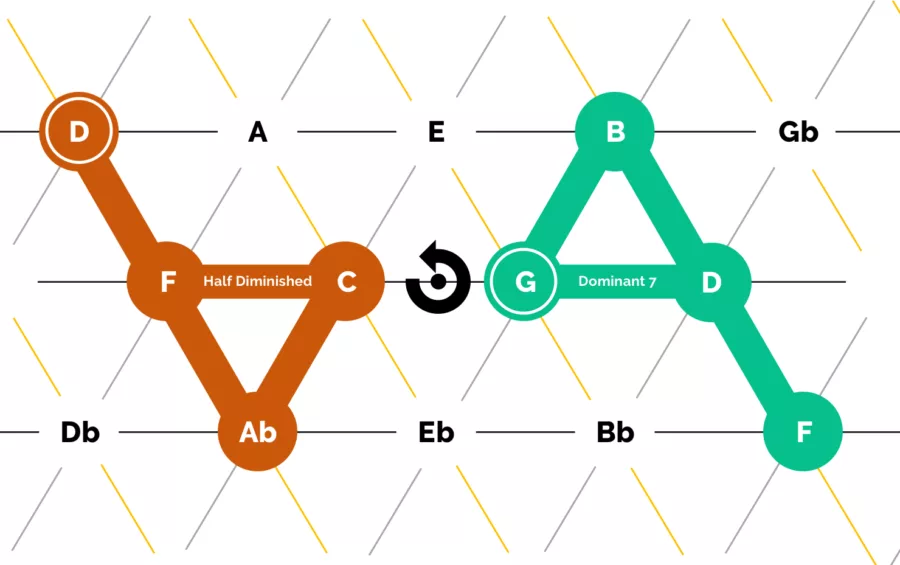
Next, we need to define the axis point, at which our negative harmony is based upon. This is often discussed as “the tonic/dominant axis.” This is a concept that confused me for a while, because the mid-point between the tonic and dominant doesn’t fall on a note. It falls between the major 3rd and minor 3rd. In this case, our axis point is between E and Eb, which is hard to understand with our traditional theory concepts. But, on the Tonnetz it’s easy. We just draw a dote halfway between C and G… done.

As our last step, to find the negative translation of the G7 dominant chord, we rotate our green chord around the axis by 180 degrees, which results in the brown D half-diminished chord.

Both of these chords have the same relative relationship to the key center, and thus have similar functions.

Try playing with this by rotating melodies and other chords around the same axis.

(I tip my hat to reddit user 4plus1 for unlocking this insight for me.)

Continued Reading #

If you are intrigued by this concept and want to drill down even further into the math behind the Tonnetz, there’s a great educational journal entry on Princeton’s website by Dmitri Tymoczko on the topic. Fair warning, it’s deep and not for the feint of heart!